Batch 3 - Class 181 - Four squares, Three jugs

• Take 4 consecutive integers and multiply them. Can you think of a sequence where the product is a perfect square?

• (Solve the homework problem)
• Ask kids to take certain sequences to test. They may start coming to the conclusion that this does not exist.
• Intuition
• How many of these numbers can be multiples of 2? Of 3? Of 4? Of 5?
• Note that none can be multiple of 5 if the product has to be a square (since at most one can be multiple of 5)
• Exactly two numbers have to be multiples of 2, and exactly one must be multiple of 4
• What does this mean in terms of prime factorization? Does it mean that the number isn't a perfect square due to 2's not adding up?
• No - because it can be a multiple of 8 as well - such as 24 and 22 - so total 4 2's in prime factorization
• Proof - through full expansion. (x-1)x(x+1)(x+2)=(x^2+x-1)^2-1, i.e. a perfect square minus 1. The difference between perfect squares only increases, so can't come back to 1.
• If you match up with the sequences above, you will notice that all of those numbers are 1 short of a perfect square.

• Problem: You have two empty jugs of 5 liter and 3 liter capacity, and a 8 liter jug full of water. All jugs are unmarked. Can you divide the water equally between two friends?
• If yes, can you determine the smallest number of steps?
• Lets now try to chart our three jug problem
• Draw the chart, and mark out areas which are not possible because jug B and C are smaller capacity
• What shape are we left with?
• If we start with (8,0,0) where will any legal pouring keep us (boundary of the parallelogram)
• What would happen if that jars were marked? We could then stop in between and not necessarily go to the boundary of parallelogram.
• Which direction will any legal pouring move us in?
• Our goal is to get to 4 liters - mark out all the points that satisfy that. Which ones are on boundary of parallelogram?
• Can you now draw a sequence of moves which get you from (8,0,0) to (4,4,0) while always moving along one of the sides, and staying on boundary of the parallelogram?
• Write down the sequence of moves and compare with your solution

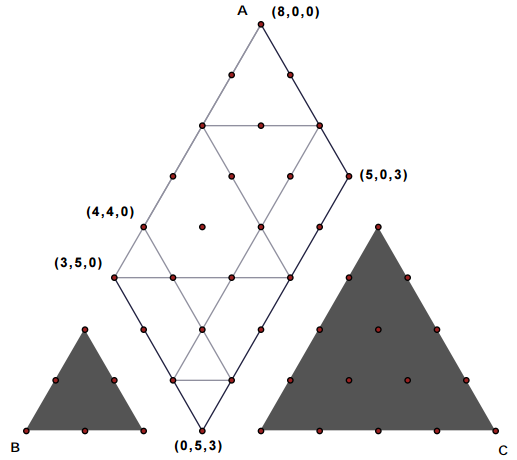
• What kind of problems are unsolvable here?
• What about any other combinations - which are the ones you can't pour out in this case?
• Lets go back to some others 
• 2,6,8 - what can you pour out?
• 4,6,10
• 5,6,11
• 6,7,8 with 10 liters of water - Can you get to 5 liters?
• Answer - No. If you draw the diagram, you will notice that all points with 5 liters form a closed triangle, which can't be reached from outside